Chapter 1 Introduction to Differential Equations Notes, Kohler & Johnson 2e

1.2 Examples of Differential Equations

Examples of differential equations:

The behavior of many physical and natural systems often involve rates of change:

Ex: Stock market, population, fluid flow, predator/prey relations, electric current, moving objects, and many others.

In calculus we saw that the rate of change is the derivative and we would write \(y'=\frac{dy}{dx}\).

A Differential Equation is an equation that contains a derivative.

TipExample 1.2.1

\(y'=3-2y\)

Note: In our typical equations the variable represents a number but in this case the variable \(y\) is actually a function of \(t\). So if we were to solve this equation we would be looking for a solution of the form \(y=f(t)\).

To solve this we need to write it in a way that we can integrate.

What we will do is we will write this in the form \(\frac{du}{u} = c \ dt\) which we can integrate as \(\ln{u} = ct + K\) where \(K\) is an arbitrary constant.

Factor a (-2) and divide to put it in a form you can integrate:

\[y'=-2\left( y-\frac{3}{2}\right)\]

You want a solution of the form \(y = f(t)\) so now we need to solve for y.

\[y = \frac{3}{2} +Ke^{-2t} \tag{1.1}\]

What about \(K\)? To solve for \(K\) you would need an initial condition such as \(y(0)=y_0\). Substitute into equation (1.1) to get:

\[y(0) = y_0 = \frac{3}{2} +Ke^{-2(0)}\]

The final solution is:

\[y = \frac{3}{2} + \left( y_0 -\frac{3}{2} \right) e^{-2t}\]

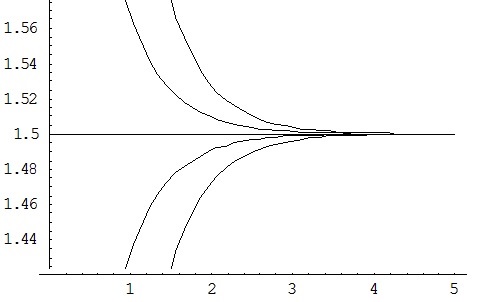
Different values of \(y_0\) will yield different solutions:

Initial Condition	Solution
\(y_0 = 0\)	\(y = \frac{3}{2} - \frac{3}{2} e^{-2t}\)
\(y_0 = \frac{3}{2}\)	\(y = \frac{3}{2}\)
\(y_0 = 2\)	\(y = \frac{3}{2} + \frac{1}{2} e^{-2t}\)
\(y_0 = 3\)	\(y = \frac{3}{2} + \frac{3}{2} e^{-2t}\)

The form of an nth order differential equation:

The previous example is a first order differential equation because it only contains a first derivative. We can have more complicated differential equations which contain higher order derivatives. The order of the differential equation is the same as the order of its largest derivative. In general we write an nth order differential equation in the form:

\[y^{(n)}=f\left(t, y, y', \ldots, y^{(n-1)}\right)\]

In this equation \(t\) is the independent variable, while \(y\) is the dependent variable. A solution of the differential equation is any function that satisfies the equation.

Two basic types:

Ordinary Differential Equations

• Only ordinary derivatives appear in the differential equation. This is primarily what we will be looking at in this class.

TipExample 1.2.2

\[t^3 \frac{d^2y}{dt^2} + t \frac{dy}{dt} +2y = \sin t\]

Partial Differential Equations

• The derivatives in the equation are partial derivatives.

TipExample 1.2.3

\[u_{xx} +u_{yy} +u_{zz}=0\]

Order

• The order of a differential equation is the order of the highest derivative that appears in the equation.

TipExample 1.2.4

In Example 2 the order of the ODE is 2.

TipExample 1.2.5

Verify that \(y(t) = (\cos t) \ln(\cos t) + t\sin t\) is a solution to the differential equation \(y'' + y = \sec t\).

TipExample 1.2.6

Verify that \(y(t) = C_1 \sin 2t + C_2 \cos 2t\) is a solution to the differential equation \(y'' + 4y = 0\), where \(C_1\) and \(C_2\) are arbitrary constants. Find values of the constants \(C_1\) and \(C_2\) so that the solution satisfies the initial conditions \(y(\pi/4)=3\) and \(y'(\pi/4)=-2\)

1.3 Direction Fields

A direction field is a way of predicting qualitative behavior of solutions to a differential equation. Let’s look at an example from the previous section.

TipExample 1.3.1

\(y'=3-2y\)

What we would like to do is to select values of \(y\) and plot values of \(y'\). Remember that \(y=f(t)\) so we will need to plot this in both the \(t\) and \(y\) directions. Since this formula is entirely in terms of \(y\) it is fairly straight forward.

\(y\)	\(\frac{dy}{dt}\)
-2	7
-1.5	6
-1	5
-0.5	4
0	3
0.5	2
1	1
1.5	0
2	-1

Direction Fields for Autonomous Equations:

Definition: Differential equations where the right hand side does not depend explicitly on \(t\) are called autonomous differential equations.

The advantage of an autonomous differential equation is that because it is not \(t\) dependent all the slopes along the line \(y = b\) are equal.

TipExample 1.3.2

\(y'=y^2-5y\)

\(y\)	\(\frac{dy}{dt}\)
-2	14
-1	6
0	0
1	-4
2	-6
3	-6
3.5	-5.25
4	-4
5	0
6	6
7	14

Equilibrium Solutions:

Consider the differential autonomous equation \(y'=f(y)\). If the real number \(\beta\) is a root of the equation \(f(y)=0\), then the constant function \(y(t) = \beta\) is a solution of \(y'=f(y)\). These constant solutions are called equilibrium solutions.

Extra examples:

TipExample 1.3.3

\(y'=-2 + t - y\)

TipExample 1.3.4

\(y'= e^{-t} +y\)