Chapter 5 Eigenvalues and Eigenvectors, Linear Algebra 6e Lay

5.1 Eigenvectors and Eigenvalues

For this section we will assume that \(A\) is an \(n \times n\) matrix. So any transformation \(T(x) = Ax\) sends vectors from \(\mathbb{R}^n\) to \(\mathbb{R}^n\).

TipExample 1

Consider the linear transformation \(T(x) = Ax\) defined by \(A = \begin{bmatrix} 4 & 1 \\ -2 & 1 \end{bmatrix}\).

1. Describe what this transformation does to the standard basis vectors in \(\mathbb{R}^2\)

2. Let \(\mathfrak{b}_1 = \begin{bmatrix} -1 \\ 1 \end{bmatrix}\). Calculate \(T(\mathfrak{b}_1)\) and describe what happens.

3. Let \(\mathfrak{b}_2 = \begin{bmatrix} -1 \\ 2 \end{bmatrix}\). Calculate \(T(\mathfrak{b}_2)\) and describe what happens.

NoteEigenvectors and Eigenvalues

NoteDefinition

An eigenvector of an \(n \times n\) matrix \(A\) is a nonzero vector \(x\) such that \(Ax = \lambda x\) for some scalar \(\lambda\). The scalar \(\lambda\) is called an eigenvalue of \(A\) if there is a nontrivial solution to the equation \(Ax = \lambda x\). (Note that an eigenvector must be nonzero but eigenvalues can be zero.)

In this section we will be given either an eigenvalue or an eigenvector for each problem.

TipExample 2

Let \(A= \begin{bmatrix} 3 & 2 \\ 3 & 8 \end{bmatrix}\). Show that \(\begin{bmatrix} 1 \\ 3 \end{bmatrix}\) is an eigenvector of \(A\). Determine the corresponding eigenvalue.

TipExample 3

Let \(A= \begin{bmatrix} 3 & 2 \\ 3 & 8 \end{bmatrix}\). Show that \(\lambda = 2\) is an eigenvalue of \(A\). Determine an eigenvector whose eigenvalue is 2.

NoteEigenspace

NoteDefinition

The set of all solutions to \((A - \lambda I) x = 0\) is a subspace of \(\mathbb{R}^n\). It is called the eigenspace of \(A\) corresponding to the eigenvalue \(\lambda\).

TipExample 4

Let \(A= \begin{bmatrix} 6 & 3 & -4 \\ 2 & 7 & -4 \\ 2 & 3 & 0 \end{bmatrix}\). If \(\lambda = 4\) is an eigenvalue of \(A\) find a basis for the eigenspace of \(A\).

NoteEigenvector Linear Independence Theorem

NoteTheorem

If \(v_1, \ldots, v_r\) are eigenvectors that correspond to distinct eigenvalues \(\lambda_1, \ldots, \lambda_r\) of an \(n \times n\) matrix \(A\), then the set \(\{v_1, \ldots, v_r\}\) is linearly independent.

TipExample 5

\(A\) is an \(m \times n\) matrix. Mark each statement TRUE or FALSE.

1. If \(Ax = \lambda x\) for some vector \(x\), then \(\lambda\) is an eigenvalue of \(A\).

2. A matrix \(A\) is not invertible if and only if \(0\) is an eigenvalue of \(A\) (\(Ax = 0x\)).

3. A number \(c\) is an eigenvalue of \(A\) if and only if the equation \((A-c I)x =0\) has a nontrivial solution.

4. To find the eigenvalues of \(A\), reduce \(A\) to echelon form.

5. If \(Ax = \lambda x\) for some scalar \(\lambda\), then \(x\) is an eigenvector of \(A\).

6. If \(v_1\) and \(v_2\) are linearly independent eigenvectors, then they correspond to distinct eigenvalues.

7. An eigenspace of \(A\) is a null space of a certain matrix.

8. An \(n \times n\) matrix can have at most \(n\) eigenvalues.

5.2 The Characteristic Equation

The Eigenvalue Problem

We would like to find solutions to \[A\vec{x} = \lambda \vec{x}\] where \(\lambda\) is a constant. In these cases multiplication by the matrix is the same as multiplication by a constant. These constants (\(\lambda\)) are called eigenvalues and their associated vectors (\(\vec{x}\)) are called eigenvectors.

So how do we find eigenvalues and eigenvectors?

We want \(A\vec{x} = \lambda \vec{x}\) so:

\[\begin{align} A\vec{x} - \lambda \vec{x} &= 0 \\ (A - \lambda I) \vec{x} &= 0 \tag{1} \end{align}\]

We know this has nonzero solutions if and only if:

\[\det(A - \lambda I)=0 \tag{2}\]

Step 1: Solve equation (2) for the eigenvalues \(\lambda\).

Step 2: The eigenvectors are the solutions to equation (1) for a particular value of \(\lambda\).

TipExample 6

Find all eigenvalues and eigenvectors for \(A = \begin{bmatrix} 1 & 3 \\ 4 & 2 \end{bmatrix}\) and find a basis for the eigenspace for the solution.

Step 1: \((A - \lambda I) = \begin{bmatrix} 1 & 3 \\ 4 & 2\end{bmatrix} - \lambda \begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix} = \begin{bmatrix} 1 - \lambda & 3 \\ 4 & 2 - \lambda \end{bmatrix}\)

\(\det(A - \lambda I)= (1 - \lambda)(2 - \lambda) - 12 =0\)

Step 2: Solve \((A - \lambda I) \vec{x} = 0\) for \(\vec{x}\)

NoteCharacteristic Equation

NoteDefinition

The equation \[\det (A-\lambda I) = 0\] is called the characteristic equation of the matrix \(A\). A scalar \(\lambda\) is an eigenvalue of an \(n \times n\) matrix \(A\) if and only if \(\lambda\) is a solution to the characteristic equation of \(A\).

TipExample 7

Find the characteristic equation of:

\[A = \begin{bmatrix}7 & -2 & -4 & -1 \\ 0 & 1 & 7& -8 \\ 0& 0 & 5 & -2 \\ 0 & 0 & 0 & 7\end{bmatrix}\]

Note that the factor \((7 -\lambda)\) and the eigenvalue \(\lambda = 7\) appear twice. The eigenvalue 7 is said to have multiplicity 2.

TipExample 8

Find the characteristic equation, the eigenvalues (\(\lambda = 3, 3\)) and the eigenvectors of:

\[A =\begin{bmatrix}2 & 1 \\ -1 & 4\end{bmatrix}\]

TipExample 9

Find the characteristic equation, the eigenvalues and the eigenvectors of:

\[A=\begin{bmatrix}4 & 0 & 0 \\ 5 & 3 & 2 \\-2 & 0 & 2\end{bmatrix}\]

Eigenvalue Properties

NoteEigenvalue Properties

Some properties of eigenvalues and eigenvectors (Eigenpairs)

1. Eigenvectors are not unique.
2. A matrix can have a zero eigenvalue
3. A real matrix may have one or more complex eigenvalues and eigenvectors.
4. Eigenvectors corresponding to distinct eigenvalues are linearly independent.

NoteThe Invertible Matrix Theorem (continued)

The Invertible Matrix Theorem (continued)

Let \(A\) be an \(n \times n\) matrix. Then the following statements are equivalent to the statements found in the Invertible Matrix Theorem given in Chapters 2 and 4 (including the statement that A is invertible):

19. The number 0 is not an eigenvalue of \(A\).

20. The determinant of \(A\) is not zero.

TipExample 10

Find the eigenvalues, eigenvectors and a basis for the eigenspace for:

\[A = \begin{bmatrix}3 & 2 & 4 \\ 2 & 0 & 2 \\ 4 & 2 & 3\end{bmatrix}\]

(Partial solution: Basis for \(E_{-1} = \left\{(1, -4, 1), (1, 0, -1)\right\}\))

5.3 Diagonalization

Diagonal matrices

Recall:

The characteristic equation of a square matrix \(A\), formally notated \(\det(A- \lambda I) = 0,\) is the equation obtained by subtracting the variable \(\lambda\) from the entries along the main diagonal of \(A\), then taking the determinant and setting it equal to zero.

The roots of this polynomial equation are the eigenvalues of \(A\). If a root is repeated \(k\) times, we say that eigenvalue has algebraic multiplicity \(k\).

TipExample 11

Find the eigenvalues and eigenvectors of:

\[A= \begin{bmatrix} 2 & 1 & 0\\ 0 & 2 & 1 \\ 0 & 0 & 2\end{bmatrix}\]

Let D be a diagonal matrix (a square matrix in which all of the entries are zero, except possibly those on the main diagonal). Then computing powers of D are simple, as this example illustrates:

TipExample 12

If \(D =\begin{bmatrix}5&0 \\ 0 & 3\end{bmatrix}\), then \(D^2 = \begin{bmatrix}5&0 \\ 0 & 3\end{bmatrix}\begin{bmatrix}5&0 \\ 0 & 3\end{bmatrix} = \begin{bmatrix}25&0 \\ 0 & 9\end{bmatrix}\)

In general, \(D^k = \begin{bmatrix}5^k&0 \\ 0 & 3^k\end{bmatrix}\).

NoteSimilar Matrices

NoteDefinition

Two matrices \(A\) and \(B\) are said to be similar if there is an invertible matrix \(P\) such that \(B=P^{-1}AP\).

If \(A\) is not a diagonal matrix itself, but it is similar to a diagonal matrix \(D\), then \(A = PDP^{-1}\), for some invertible matrix \(P\). Then:

\[A^2 = (PDP^{-1})(PDP^{-1}) = PD^2 P^{-1}\]

In general, \(A^n = PD^n P^{-1}\).

Compare the number of multiplications required to compute each side of this equation when \(n\) is very large, and you’ll see that this formula can be quite efficient.

NoteEigenvalue Properties

NoteTheorem

If \(A\) and \(B\) are similar they have the same eigenvalues. (Note: This does NOT work in the other direction.)

Diagonalizability

NoteDiagonalizable

NoteDefinition

A square matrix \(A\) is said to be diagonalizable if \(A = PDP^{-1}\) for some diagonal matrix \(D\).

NoteTheorem

An \(n \times n\) matrix \(A\) is diagonalizable if and only if \(A\) has \(n\) linearly independent eigenvectors. In other words, \(A\) is diagonalizable if and only if the eigenvectors of \(A\) form a basis for \(\mathbb{R}^n\).

If this is the case, then the columns of \(P\) are the eigenvectors of \(A\), and the diagonal entries of \(D\) are the eigenvalues of \(A\), in corresponding order.

TipExample 13

Diagonalize \(A= \begin{bmatrix}3 & 2 & 4 \\ 2 & 0 & 2 \\ 4 & 2 & 3\end{bmatrix}\). We did the work in example 10.

TipExample 14

Diagonalize \(A=\begin{bmatrix} 2 & 1 & 0\\ 0 & 2 & 1 \\ 0 & 0 & 2\end{bmatrix}\). We did the work in example 11.

5.5 Complex Eigenvalues

Complex Arithmetic

Q: What is a complex number?

A: It is a number of the form \(a + bi\) where \(a\) and \(b\) are real numbers and \(i^2 = -1\).

• \(a\) is called the real part
• \(b\) is called the imaginary part.
• The conjugate of \(a + bi\) is \(a - bi\).

Properties

1. \(a + b~i = c + d~i \qquad \Leftrightarrow \qquad a = c ~ \text{and} ~ b = d\)
2. \((a + b~i) + (c + d~i) = (a + c) + (b + d)~i\)
3. \((a + b~i) \cdot (c + d~i) = ac + ad~i + bc~i +bd~i^2 = (ac-bd)+(ad+bc)~i\)
4. \((a+b~i)(a-b~i) = a^2 + b^2\)

TipExample 15

1. \(\displaystyle \frac{i}{3+i}\)

2. \(\displaystyle \frac{3-5i}{2-i}\)

3. \((3-\sqrt{-4})+(-8+\sqrt{-25})\)

4. \(\displaystyle \frac{1}{3i}\)

Complex Numbers in Equations

TipExample 16

Solve for \(x\): \(x^2 + 1 = 0\)

TipExample 17

Solve the system of equations:

\(x_1 + i x_2 = 0\)

\((1-i)x_1 + (1+i) x_2 = 0\)

TipExample 18

Find the eigenvalues and eigenvectors of \(\begin{bmatrix} 5 & -2 \\ 1 & 3 \end{bmatrix}\)

TipExample 19

Find the eigenvalues and eigenvectors of \(\begin{bmatrix} -5 & -5 \\ 5 & -5 \end{bmatrix}\)

Polar Form of a Complex Number

NoteEuler’s Formula

Euler’s Formula

\[\begin{align*} e^{i\theta} & = \cos \theta + i \sin \theta \\ e^{-i\theta} & = \cos (-\theta) + i \sin (-\theta) \\ & = \cos \theta - i \sin \theta \end{align*}\]

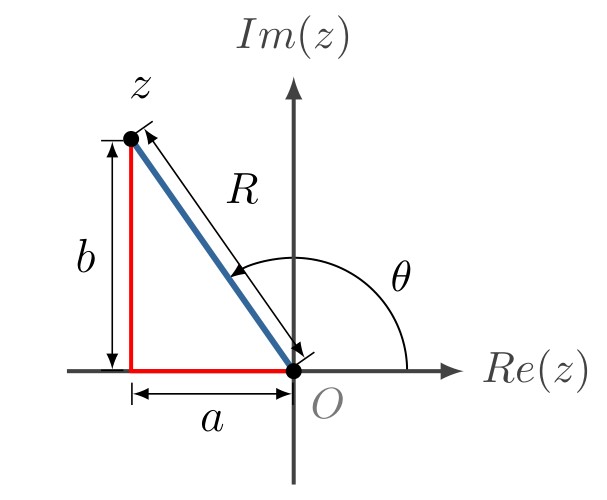
Euler’s formula allows us to plot complex numbers on the Re-Im plane. This is called an Argand Diagram. For example for a complex number of the form \(z=a+bi = Re^{i\theta}\) the Argand Diagram is shown below.

TipExample 20

If \(C = \begin{bmatrix} a & -b \\ b & a \end{bmatrix}\), where \(a\) and \(b\) are nonzero real numbers, then the eigenvalues of \(C\) are \(\lambda = a \pm bi\). Show that \(C\) can be written as a scale factor matrix \(\begin{bmatrix} r & 0 \\ 0 & r \end{bmatrix}\) where \(r = |\lambda|\) and a rotation matrix \(\begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix}\) where \(\theta\) is the angle between the positive \(x\)-axis and the vector \([a, b]\).

Solution:

\[C = r \begin{bmatrix} a/r & -b/r \\ b/r & a/r \end{bmatrix}\]